10th Computer Chapter 6
Chapter 6: Computer Logic and Gates
Write short answers to the following questions
i. What is a logic gate?
Answer:
Logic gates are the basic building blocks of digital computers. Logic gates operate on two voltage levels and process digital signals, which represent binary digits 0 and 1.
ii. Define the truth table.
Answer
Truth Table
A truth table represents a digital logic circuit. It shows the output for all the possible combinations of inputs using 0 for LOW and 1 for HIGH. All the combinations of inputs are listed in columns on the left and the output is shown in the rightmost column of the table.
iii. Define Boolean function.
Answer
Boolean Function
A Boolean function is an expression formed with binary variables, the logical operators (OR, AND and NOT), parenthesis and equal sign. A binary variable can take the value of 0 or 1. For a given value of the variables, the function can be either 0 or 1.
iv. What is Karnaugh map and why is it used?
Answer
Karnaugh Map
K-map is a pictorial form of a truth table. It consists of square boxes called cells. All the possible combinations of variables involved in a Boolean function are written inside the cells in their respective positions. A two-variable K-map contains 22=4 cells, a three-variable 23=8 cells and so forth.
Use of K-map
K-map is used to simplify Boolean algebra expressions.
v. Draw a three-variable Karnaugh map for variables X, Y and Z.
Answer
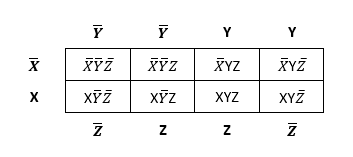
EXTENSIVE QUESTIONS
Q3. Draw the graphical symbols of AND, OR, NOT, NAND and NOR gates and write their functions.
AND Gate

The AND gate operates such that the output will be at level 1 (HIGH) only when all inputs are 1 (HIGH). The mathematical expression for the two-input AND gate is written as F=xy. For a three-input gate, it would be F=xyz, and so on for more inputs.
OR Gate

The OR gate produces a 1 output when any input is 1. Its mathematical expression is F=x+y, where the + stands for the OR operation and not normal addition. For a three-input OR gate, it would be F=x+y+z, and so on.
NOT Gate

A NOT gate is a single Input gate. It converts LOW to HIGH and vice versa. Its logic expression is F=x ̅. The bar in the expression indicates the inversion operation. In the output of the graphical symbol, the small circle indicates inversion.
NAND Gate

The NAND gate combines the AND and NOT gates, such that the output will be 0 only when all the inputs are 1. Its logic expression is F=(xy) ̅ which indicates that inputs x and y are first ANDed and then the result is inverted. Inversion is indicated by a bar. Thus, an AND gate always produces an output that is the inverse (opposite) of an AND gate.
NOR Gate
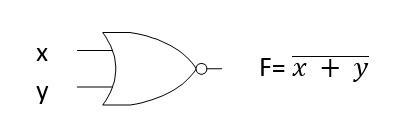
The NOR gate combines the OR and NOT gates, such that the output will be 0 when any input is 1. Its logic expression is F = (x+ y) ̅, which indicates that x and y are first ORed and then the result inverted. A bar indicates inversion. A NOR gate always gives an output that is the inverse of an OR gate.
O4. Explain how NAND and NOR gates can be created using AND, OR and NOT gates.
Answer
The NAND gate combines the AND and NOT gates, such that the output will be 0 only when all the inputs are 1. Its logic expression is F = (xy) ̅ which indicates that inputs x and y are first ANDed and then the result is inverted. A bar indicates inversion. Thus, an. AND gate always produces an output that is the inverse (opposite) of an AND gate.

The NOR Gate
The NOR gate combines the OR and NOT gates, such that the output will be 0 when any input is 1. Its logic expression is F=(x+y) ̅, which indicates that x and y are first ORed and then the result inverted. A bar indicates inversion. A NOR gate always gives an output that is the inverse of an OR gate.

Q5. Draw the truth table of the following Boolean functions.

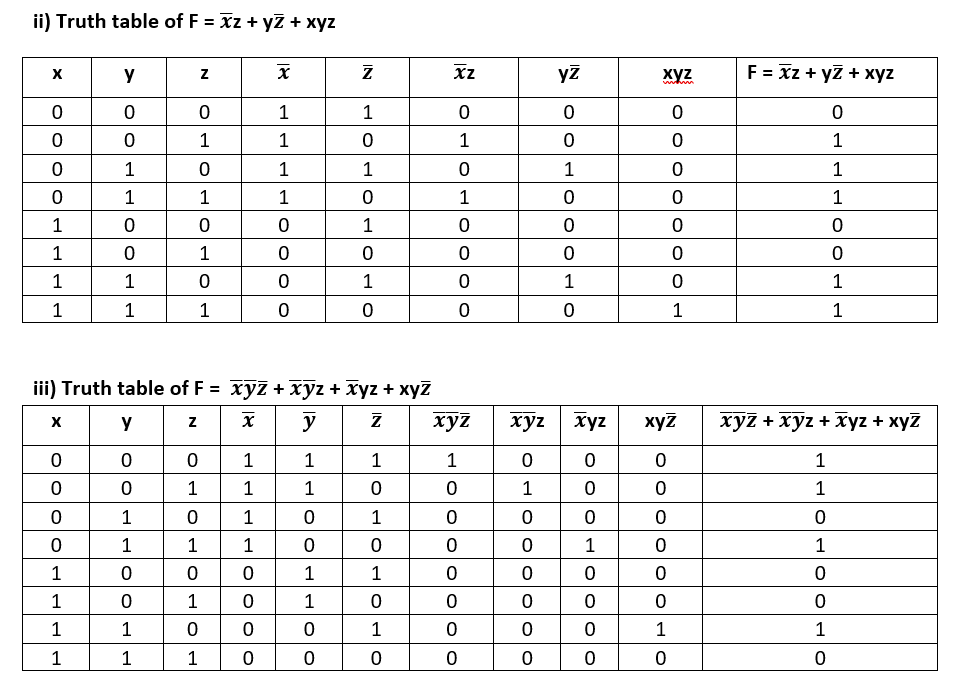





Q7. Draw the logic circuits of the following Boolean functions.



Select the best answer for the following MCQs.
- Which operation is represented by the “+” sign?
a) AND
b) OR
c) NOT
d) NAND - Which operation is represented by a dot or the absence of an operator?
a) AND
b) OR
c) NOT
d) NAND - Which of the following gates is also known as inverter?
a) OR gate
b) NOR gate
c) NAND gate
d) NOT gate - Which combination of inputs to a two-input AND gate will produce an output of HIGH?
a) LOW and LOW
b) LOW and HIGH
c) HIGH and HIGH
d) None of these - Which logic gate is represented by the function, F = ((x + y) ̅) ?
a) NAND
b) NOR
c) Exclusive-OR
d) Exclusive-NOR - Which logic gate is represented by the function, = ((xy) ̅)?
a) NAND
b) NOR
c) Exclusive-OR
d) Exclusive-NOR - What is the maximum number of possible input combinations in a truth table that has three variables?
a) 3
b) 6
c) 8
d) 9 - How many AND gates are required to create the logic circuit of the Boolean function:
F=x ̅z+ yz ̅+xyz?
a) 1
b) 2
c) 3
d) 4
